Fake Tweets
Network Description
There are different clusters, most of them are form according to the language of nodes.
Two very self contained clusters are the german (orange, upper middle) and the spanish cluster (turquoise, middle right).
They stand in contrast to the russian cluster, which is very interconnected with a lot of english accounts.
However, there is also a completely seperate english cluster forming on the lower right, without a lot of accounts from different languages.
For comparison, the same plot, but according to the communities (found using the louvain algorithm can be found here).
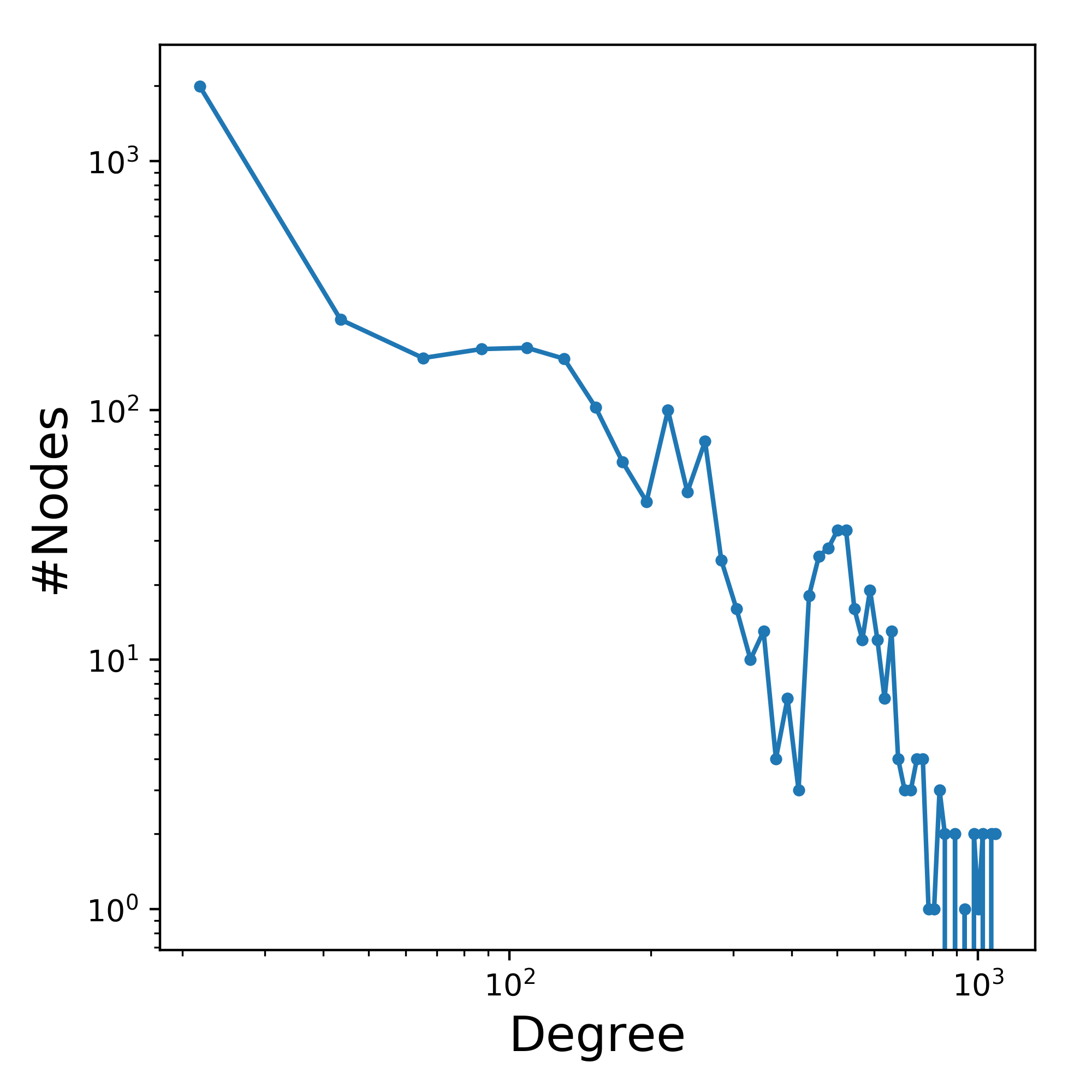
Subnetwork > 1000 Follower
Because of the network size, this uses WebGL backend of plotly, might therefore look ugly on high-res displays. You can open the
Subnetwork in a separate window.
Since this network is very big, and makes exploration of the relationshib between the differen accounts very difficult, a spereate network was created for just accounts with more than 1000 followers.
Analyzing the community structure
The accounts have 11 different languages, of these are (language-code, with the according number of nodes): [('ar',28), ('de',111), ('en',2286), ('en-gb', 11), ('es',194), ('fr',11), ('id',1), ('it',7), ('ru',1013), ('uk',2), ('zh-cn',3)]
The value for the modularity based on the languages is $\approx 0.08$.
So while the modularity is still positive, it is still very small, especially compared to the modularity for the communities found using the louvain-algorithm: $\approx 0.43$.
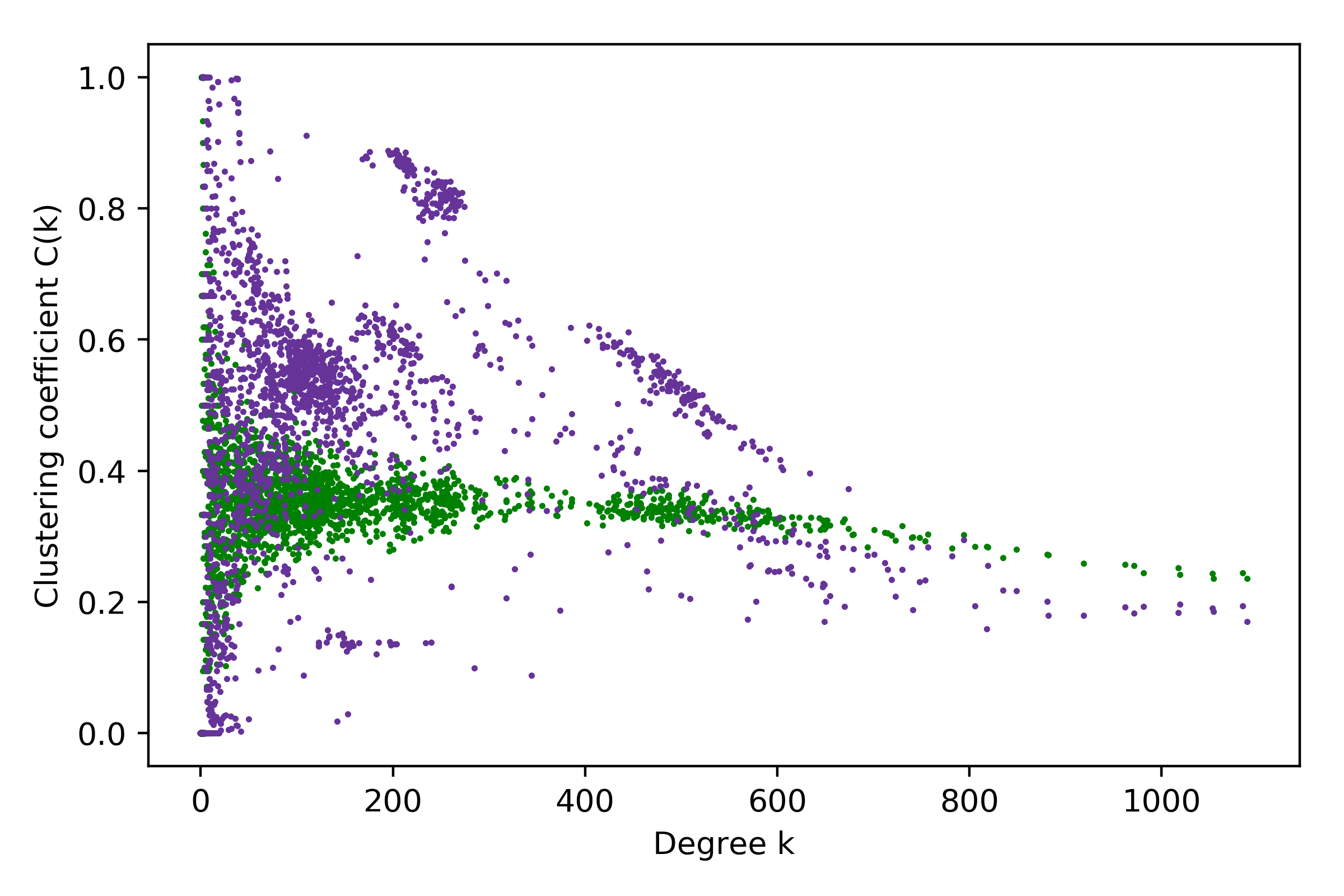
To get a sense of how good the languages correspond to the communities calculated through the louvain-algorithm, the confusion matrix was calculated (communities with less than 2 members were disregarded).
For the 3 big language-communities, the following results were found:
'de': $98\%$ were in the same community.
This further verifies that the community of german-troll accounts is very clustered and fairly disconnected from the rest of the troll-network.
'en': $55\%$ are in the same/biggest community.
However, the rest is not spaced out evenly, but there is a seccond subcommunity forming with, and together they correspond to $66\%$ of the nodes with language 'en'.
'es': $44\%$ are member of the biggest community.
However, there is a second, equally big community, which also has mostly just 'es' members, together they correspond to $75\%$ of the 'es'-nodes.
'ru': $43\%$ are member of the biggest community.
However, this community is overlapping quiet a lot with a 'en'-community ($396$ nodes are 'ru' and $91$ are 'en'.)
3 of the 4 other big 'ru' communites are also overlapping quiet a bit with 'en' communities, however, there is one community with $89$ members, that has only $7$ 'en' members.
Conclusion
The 'de' (german) and the 'es' (spanish) are quiet clustered, however, the 'en'(english) and 'ru'(russian) community are both quiet intertwined with each other.
However, this might also be due to the fact, that they are the quiet a bit bigger than the german and spanish one.